براكسيلابس المدونة العربية لمعامل العلوم الإفتراضية براكسيلابس
تعتبر معادلة برنولي أو معادلة طاقة التدفق الثابت غير القابلة للضغط واحدة من أكثر المعادلات شهرة في الفيزياء (ميكانيكا الموائع) التي تشرح مبدأ حفظ طاقة العمل الميكانيكية لتدفق سائل. نشرت المعادلة عام 1738 بواسطة دانيال برنولي -عالم فيزياء سويسري ولد في 8 فبراير 1700 في هولندا ودرس الرياضيات والطب – لمساعدتنا على فهم تدفق السوائل.
في هذا المقال سنتناول مبدأ برنولي والصيغة الرياضية للقانون وأشهر التطبيقات المختلفة للمعادلة.
ابدا تجربتك الان فى معامل براكسيلابس ثلاثيه الابعاد!
معادلة برنولي
تصف نظرية برنولي العلاقة بين السرعة والضغط والارتفاع لسائل متدفق في خط انسيابي. و تنص على أن الضغط الديناميكي بالإضافة إلى الضغط الساكن في التدفق ، نصف الكثافة (r) مضروبة في السرعة (V) ، يساوي ثابتًا في جميع أنحاء التدفق. يسمى الثابت بالضغط الكلي للتدفق (pt).
أو بشكل أبسط يمكننا القول أن معادلة برنولي تنص على أن مجموع الطاقات المحتملة والحركية والتدفق للسائل يكون ثابت في خط انسيابي في تدفق ثابت.
ملحوظة:
الانسياب في التدفق الثابت هو المسار الذي يتتبعه جسيم واحد داخل المائع.
الصيغة الرياضية لمعادلة برنولي
تعتبر صيغة معادلة برنولي بمثابة علاقة بين الضغط والطاقة الكامنة والطاقة الحركية للسائل.
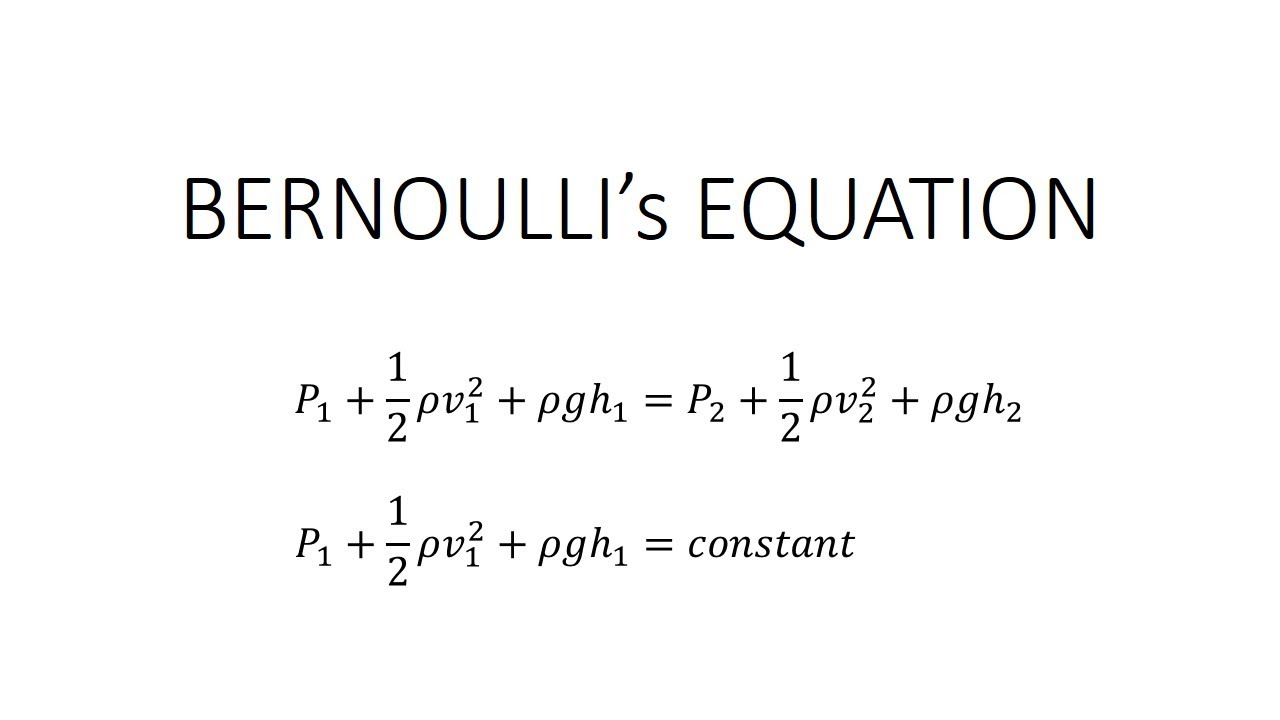
توضح المعادلة السابقة الصيغة الرياضية لمعادلة برنولي، حيث:
P هو الضغط الساكن (ضغط السائل)
ρ هي الكثافة
V هي السرعة
G هو عجلة الجاذبية
H هو ارتفاع السائل
لتطبيق معادلة برنولي
- يجب أن يكون التدفق الانسيابي ثابتًا. (يجب ألا تتغير السرعة والكثافة والضغط في أي وقت أثناء الانسياب).
- يجب أن يكون التدفق غير قابل للضغط ، حتى عندما يتغير الضغط ، يجب أن تظل الكثافة ثابتة على طول الخط الانسيابي.
- يجب أن يكون الاحتكاك بالقوى اللزجة ضئيلاً.
باستخدام التدفق غير القابل للضغط ، سيكون لدينا أبسط شكل من قانون برنولي كما هو موضح.
ما هو مبدأ برنولي؟
ينص مبدأ برنولي على أن الزيادة في السرعة (سرعة تدفق السائل) تحدث في وقت واحد ويجب أن تكون مصحوبة بانخفاض في الطاقة الكامنة للسائل (أو الضغط الساكن).
يمكن اشتقاق مبدأ برنولي من مبدأ الحفاظ على الطاقة. في حالة التدفق الثابت ،سيبقى مجموع أشكال الطاقة في السائل كما هو في جميع نقاط هذا الانسياب. بينما تظل كل الطاقة ثابتة ، فإن الزيادة في سرعة السائل تعني أن هناك زيادة في الطاقة الحركية أو الضغط الديناميكي. يحدث هذا مع انخفاض في الطاقة الكامنة (الضغط الساكن والطاقة الداخلية).
يمكن اعتبار معادلة برنولي بمثابة مبدأ حفظ الطاقة للسوائل المتدفقة، وتأثير برنولي هو خفض ضغط السائل في الحالات التي تزداد فيها سرعة التدفق.
قيود استخدام نظرية برنولي
تنطبق معادلة برنولي على التدفق الثابت كما أوضحنا من قبل ، ولكن في بعض الحالات لا يمكننا استخدام معادلة برنولي:
- لا تنطبق نظرية برنولي في التدفق لبعض الآلات (على سبيل المثال: المروحة أو التوربينات أو المضخة) ، لأن هذه الآلات يمكن أن تلحق الضرر بخطوط الانسياب وتحدث تفاعلات للطاقة مع السائل. لذلك في هذه الحالات ، يجب استخدام معادلة الطاقة بدلاً من معادلة برنولي.
- لا ينبغي أيضًا استخدام المعادلة لأقسام تدفق تغير درجة الحرارة بشكل كبير مثل أقسام التبريد أو التسخين ، لأن كثافة الغاز تتناسب عكسياً مع درجة الحرارة.
- يتضمن كل تدفق بعض الاحتكاك ولكن ان لم تكن تأثيرات الاحتكاك ضئيلة ، فإن نظرية برنولي لا تنطبق في هذه الحالة.لذلك ،
- لا ينبغي استخدام معادلة برنولي في تدفق : في حالة التمدد المفاجئ \ جزء التدفئة \ صمام \ المروحة\أنبوب طويل ضيق
تمكّنك معامل العلوم الافتراضية من براكسيلابس من إجراء تجارب معملية متنوعة في الفيزياء والكيمياء والبيولوجيا عبر الإنترنت في أي وقت وفي أي مكان. قم بإنشاء حسابك المجاني وجرب المعامل الافتراضية
ابدا تجربتك المعمليه عبر الانترنت الان!
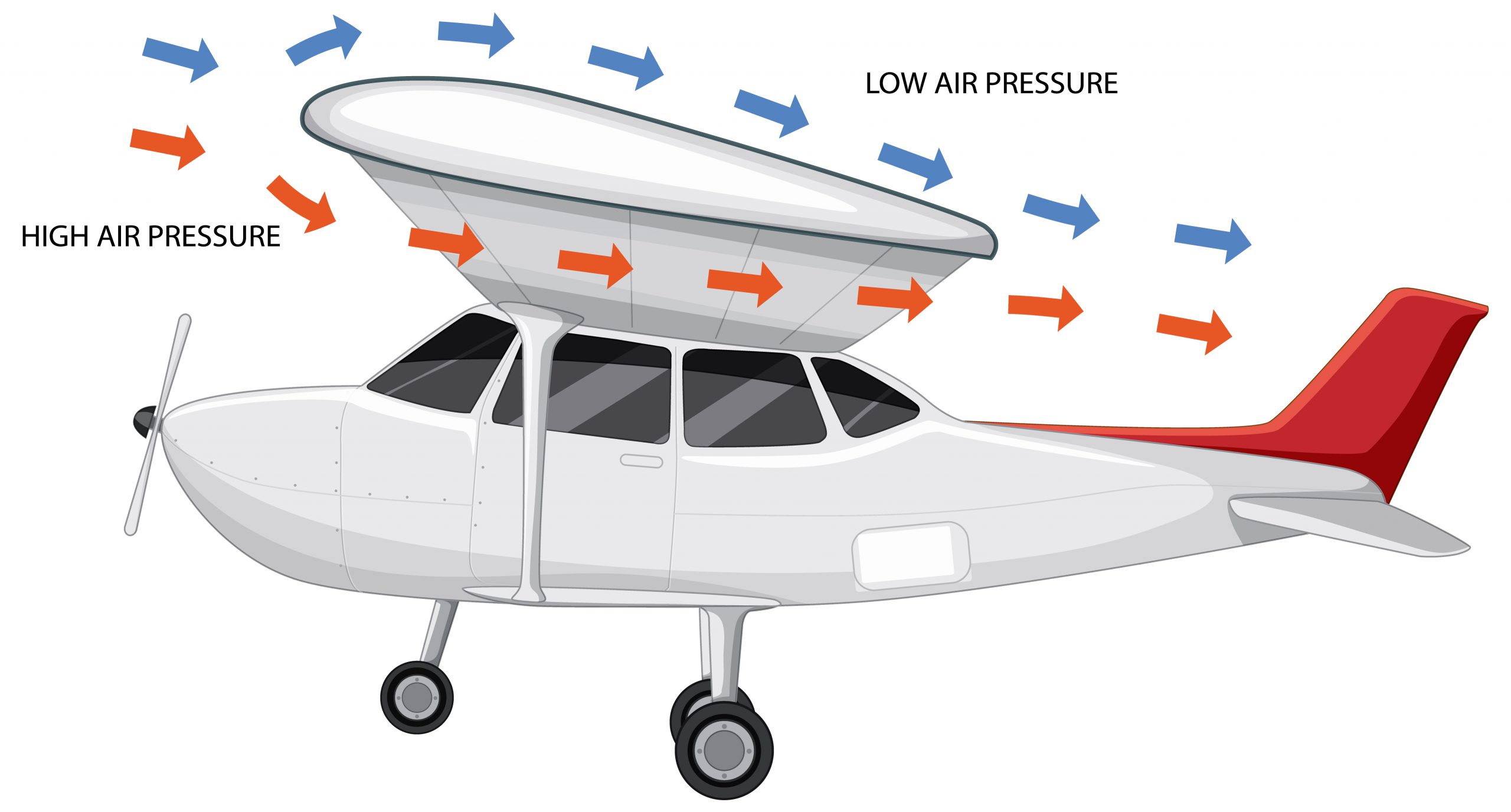
قانون برنولي للطيران
يمكن تفسير كيف تولد اجنحة الطائرات قوة الرفع من خلال قانون برنولي للسوائل؛ ففي حالة الطيران ينتقل المائع المتدفق فوق جناح الطائرة بسرعة أكبر من المتدفق تحت الجناح، و وفقا لمبدأ برنولي هذا يتسبب في انشاء منطقة من الضغط المنخفض فوق سطح الهواء ومنطقة من الضغط المرتفع تحت الطائرة وهذا الفرق في الضغط هو الذي يولد الارتفاع.
أي يمككنا تفسير سبب شكل الأجنحة وانحناءها لاعلى (طبقا لنظرية برنولي) أن الهواء يمر بسرعة أعلى على السطح العلوي من السطح السفلي. يتم حساب الفرق في سرعة الهواء باستخدام مبدأ برنولي لإحداث فرق في الضغط.
تطبيقات معادلة برنولي
معادلة برنولى لها الكثير من التطبيقات، فمثلا يمكننا استخدامها لتفسير كيف تولد الطائرات قوة الرفع أو لحساب سرعة تدفق الموائع أو سبب اضطرار السفن إلى الهرب بعيدًا عن بعضها البعض أثناء مرورها وغيرها من التطبيقات التى تصادفنا في حياتنا اليومية. سنتناول بالتفصيل بعض من أشهر هذه التطبيقات.
كيف يتم تطبيق معادلة برنولي في ميكانيكا الموائع؟
يتم تطبيق معادلة برنولي على جميع مشاكل تدفق السوائل غير القابل للضغط. يمكن تطبيق معادلة برنولي على أجهزة القياس التالية مثل مقياس فنتوري، ومقياس الفوهة ، وأنبوب Pitot وتطبيقاته لقياس التدفق من داخل الأنابيب وكذلك في القنوات المفتوحة.
كيف يتم تطبيق معادلة برنولي في المضخات؟ (قانون برنولي للسوائل)
يمكن حساب أقصى معدل تصريف ممكن لخزان به فتحة أو صنبور في القاعدة مباشرة من خلال معادلة برنولي ، وقد وجد أنه يتناسب مع الجذر التربيعي لارتفاع السائل في الخزان (هذا هو قانون توريتشيلي)وهذا يوضح أن قانون توريتشيلي متوافق مع مبدأ برنولي. تقلل اللزوجة من معدل التصريف.
تطبيق معادلة برنولي لايجاد الضغط المجهول
في مشاكل معينة في تدفقات السوائل ، نعرف السرعات عند نقطتين من الانسياب والضغط عند نقطة واحدة. المجهول هو ضغط السائل عند النقطة الأخرى. في مثل هذه الحالات (إذا استوفوا الشرط المطلوب لمعادلة برنولي) يمكننا استخدام معادلة برنولي للعثور على الضغط غير المعروف. أحد الأمثلة على ذلك هو:
التدفق عبر فوهة: يدخل التدفق إلى الفوهة بسرعة منخفضة ، ويتسارع ويترك الفوهة عند الضغط الجوي. علينا إيجاد الضغط عند المدخل. في هذه الحالة يمكننا ببساطة تطبيق معادلة برنولي بين نقاط الدخول والخروج وحساب الضغط المجهول على افتراض أن التغيير في الارتفاع يساوي الصفر.
تطبيق معادلة برنولى لايجاد السرعة المجهولة
في المسائل التي يُعرف فيها الضغط والارتفاع عند نقطتين والسرعة عند نقطة واحدة ، وعلينا إيجاد السرعة المجهولة ، يتم تطبيق معادلة برنولي لحساب السرعة المطلوبة. أحد الأمثلة على ذلك هو
التدفق عبر السيفون: يستخدم السيفون لتصريف السائل من الخزان عند مستوى أعلى إلى مستوى أدنى. مطلوب هنا إيجاد السرعة التي يغادر بها السائل السيفون. نطبق معادلة برنولي بين سطح الخزان ونقطة خروج السيفون حيث يترك السائل الأنبوب. الضغط في كلا النقطتين هو نفسه (ضغط الغلاف الجوي) ، والسرعة في الخزان لا تكاد تذكر وذلك لأن الخزان كبير.
يمكن حساب السرعة عند نقطة الخروج باستخدام قيم الارتفاع عند النقطتين. أي يمكننا أن نقول إن الانخفاض في الارتفاع أو الرأس المحتمل يظهر على أنه سرعة السائل عند نقطة خروج أنبوب السيفون.
التطبيقات الأخرى لمبدأ برنولي هي:
- تُستخدم نظرية برنولي لدراسة التدفق المحتمل غير المستقر المستخدم في نظرية موجات سطح المحيط والصوتيات.
- من تطبيقات معادلة برنولي أيضا أنه عندما نقف في محطة سكة حديد ويأتي قطار ، فإننا نميل إلى السقوط نحو القطار. يمكننا تفسير ذلك باستخدام مبدأ برنولي ؛ فعند مرور القطار ، تزداد سرعة الهواء بيننا وبين القطار. ومن ثم ، من المعادلة ، يمكننا القول أن الضغط يتناقص. لذا فإن الضغط من الخلف يدفعنا نحو القطار وهذا يعتمد على تأثير برنولي.
- تفسر معادلة برنولي أيضا كيفية عمل موقد لهب بنزن فعند فتح صمام الغاز، يتدفق الغاز الى البرميل بسرعة متجهة عالية و وفقا لنظؤية برنولي فان هذه السرعة المتجهة العالية تصنع منطقة ذات ضغط منخفض في البرميل (والتي تستمد الهواء من خلال المنظم) مما يسمح بحرق الغاز بشكل كامل أكثر.
- تعتمد الكثير من أجهزة قياس التدفق على مبدأ برنولي لتحديد السرعة المتجهة للمائع المتدفق، من أشهر هذه الأجهزة هي Pitot- Static Tube الذي يستخدم في الطائرات لقياس سرعة الطيران.
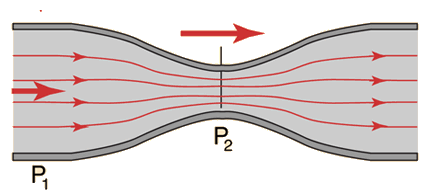
- من الاجهزة الاخرى التي تعتمد على مبدأ برنولي هو مقياس فنتوري وهو جهاز يستخدم لتحديد معدل التدفق من خلال انبوب، وهويعمل عن طريق قياس خفض الضغط pressure drop عبر مقطع قريب من الانبوب. بالنسبة للسائل غير القابل للضغط ، سيؤدي تقليل القطر إلى زيادة سرعة تدفق السائل. بعد ذلك ، يوضح مبدأ برنولي أنه يجب أن يكون هناك انخفاض في الضغط في منطقة القطر المخفض. تُعرف هذه الظاهرة باسم تأثير الفنتوري.
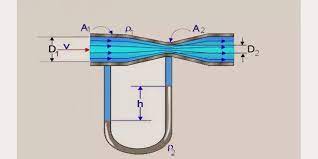
مقياس فنتوري
- ينطبق مبدأ برنولي أيضًا على تأرجح كرة الكريكيت. خلال المباراة ، يقوم اللاعبون باستمرار بتلميع جانب واحد من الكرة. بعد مرور بعض الوقت ، يكون أحد الجانبين خشنًا تمامًا والآخر لا يزال أملسًا. ومن ثم ، فعند رمي الكرة في الهواء ، تكون السرعة على أحد جانبي الكرة أسرع من الأخرى ، بسبب هذا الاختلاف في النعومة ، وهذا يؤدي إلى اختلاف الضغط بين الجانبين ؛ مما يؤدي إلى دوران الكرة (“التأرجح”) أثناء انتقالها في الهواء.
تمكّنك معامل العلوم الافتراضية من براكسيلابس من إجراء تجارب معملية متنوعة في الفيزياء والكيمياء والبيولوجيا عبر الإنترنت في أي مكان وفي أي وقت. قم بإنشاء حسابك المجاني وجرب المعامل الافتراضية الخاصة بنا.
