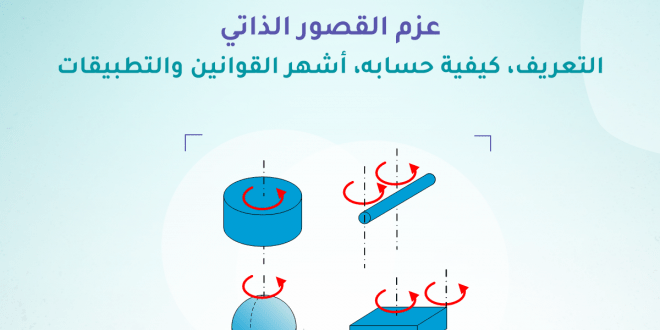
يعد مبدأ القصور الذاتي أحد المبادئ الأساسية في الفيزياء الكلاسيكية التي لا تزال تستخدم حتى اليوم لوصف حركة الأشياء وكيف تتأثر بالقوى المطبقة عليها.
على سطح الأرض، غالبًا ما يتم إخفاء القصور الذاتي عن طريق الجاذبية وتأثيرات الاحتكاك ومقاومة الهواء ، وكلاهما يميل إلى تقليل سرعة الأجسام المتحركة (عادةً إلى نقطة السكون). و القصور الذاتي خاصية سلبية ولا تمكن الجسم من فعل أي شيء باستثناء معارضة العوامل النشطة مثل القوى وعزم الدوران.
سنتنحدث في هذا المقال عن عزم القصور الذاتي وكيفية حسابه وأهم معادلاته وتطبيقاته المختلفة.
أكتشف خطط الإشتراكات المتاحة لدي براكسيلابس
ما هو تعريف القصور الذاتي Inertia؟
لنفهم عزم القصور الذاتي، يجب أن نفهم أولا ما هو القصور الذاتي.
من خلال قانون نيوتن الأول للحركة، دائما يكون الجسم لديه ميل للبقاء في حالة راحة أو في حركة موحدة. تُعرف خاصية الجسم هذه بالقصور الذاتي. وبالتالي، فإن القصور الذاتي هو خاصية الجسم التي يعارض أو يقاوم بسببها أي تغيير في حالة الراحة أو الحركة الموحدة.
يمكن الإشارة إلى مصطلح القصور الذاتي على أنه “مقدار مقاومة الجسم لتغير السرعة” أو “مقاومة التغيير في الحركة”. يتضمن ذلك التغييرات في سرعة الجسم أو اتجاه الحركة. و أحد جوانب هذه الخاصية هو ميل الأشياء إلى الاستمرار في التحرك في خط مستقيم بسرعة ثابتة، عندما لا توجد قوى تؤثر عليها.
عرّف إسحاق نيوتن القصور الذاتي على أنه:
(القوة الجوهرية للمادة هي قوة المقاومة التي يسعى من خلالها كل جسم بقدر ما يكمن فيه، إلى الحفاظ على حالته الحالية، سواء كان ذلك في حالة سكون أو التحرك بشكل موحد للأمام في خط مستقيم)
يمكننا اختصار الأمر كالتالي:
تزداد القوة اللازمة لبدء حركة الجسم من السكون، كلما زادت كتلته. أو بعبارة أخرى، فإن القصور الذاتي يزداد بزيادة الكتلة.
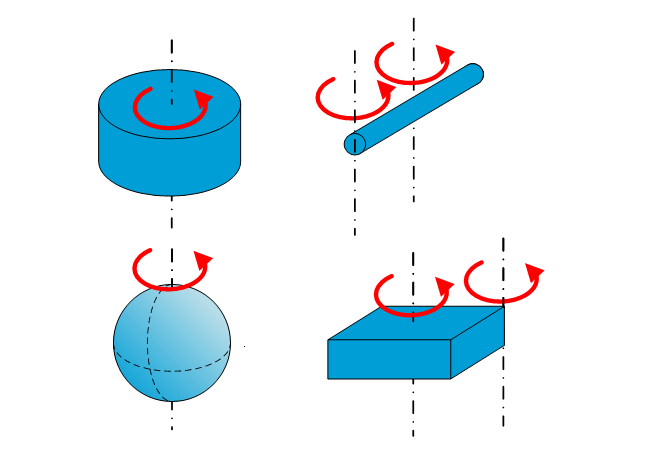
عزم القصور الذاتي Moment of Inertia
العزم في الفيزياء هو نتيجة الكتلة مضروبة في مسافة معينة من نقطة الارتكاز أو المحور؛ وبذلك يمكن تعريف عزم القصور الذاتي رياضياً بأنه ناتج كتلة الجسم مضروب بمربع المسافة من نقطة تم فيها التأثير عليه بقوة معينة؛ بحيث كلما زاد القصور الذاتي للجسم، زادت الحاجة إلى المزيد من العزم ليتم تغيير اتجاه حركته، أو إيقافه، كما يتناسب عزم القصور الذاتي تناسباً طردياً مع سرعة الجسم وكتلته.
أي أن عزم القصور الذاتي في الفيزياء هو مقياس كمي للقصور الذاتي الدوراني للجسم، أي عندما يقاوم الجسم سرعة دورانه حول محور الدوران، وتنتج هذه السرعة من تطبيق عزم الدوران على الجسم، ويكون المحور الذي يدور حوله الجسم داخليًا أو خارجيًا، ثابتًا أو متغيرًا. ومع ذلك ، يتم دائمًا تحديد لحظة القصور الذاتي فيما يتعلق بهذا المحور. ويتم تعريفها على أنها مجموع النتائج التي تم الحصول عليها بضرب كتلة كل جسيم من المادة في جسم معين في مربع المسافة من المحور .
يعتمد عزم القصور بالأساس على عدة عوامل وهي:
كتلة الجسم:
طريقة توزيع الكتلة بالنسبة لمحور الدوران؛ فعندما يضم متزلج الجليد يديه للداخل فإنّ كتلته لا تتغير وتبقى ثابتة، لكن عزم القصور الذاتي لديه يتناقص بسبب توزيع الكتلة.
اتجاه محور الدوران:
المسافة العمودية من المحور إلى مركز الكتلة، والذي يعد من أهم العوامل المؤثرة على عزم القصور، فقيمته تكون أعلى ما يمكن عندما تتوزع كتلة الجسم بعيدًا عن محور الدوران.
حساب عزم القصور الذاتي Moment of Inertia
يمكن حساب عزم القصور الذاتي لأي جسم له شكل يمكن وصفه بواسطة صيغة رياضية عادةً عن طريق حساب التفاضل والتكامل لهذا الجسم.
أما بالنسبة للجسم الذي له شكل لا يوصف رياضيًا، يمكن حسابه عن طريق التجربة.
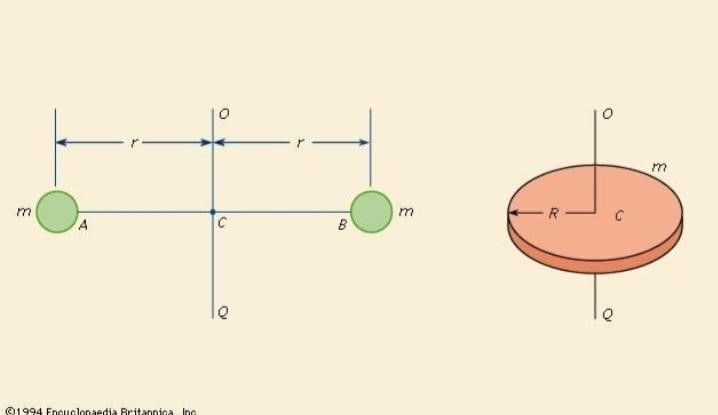
فمثلًا توظف إحدى التجارب العلاقة بين زمن تأرجح البندول الملتوي وعزم القصور للكتلة المعلقة. لنفترض أن القرص في الشكل السابق عُلّق بسلك OC مثبت عند O، فإذا بُرِم ثم تحرر سوف يتأرجح حول OC. ويعتمد زمن التأرجح الكامل على كلا من صلابة السلك وعزم القصور الذاتي الناشئ في القرص؛ وبالتالي كلما كان القصور الذاتي أكبر كان الوقت أطول.
سنتناول المزيد من التفاصيل عن حساب و قوانين عزم القصور الذاتي في الفقرات التالية..
قوانين Moment Of Inertia عزم القصور الذاتي
عزم القصور يستخدم للتعبير عن الكمية الفيزيائية المطلوبة لتغيير سرعة جسم يتحرك دائريًا حول محور ما، وقد تتغير قيمة عزم القصور لنفس الجسم بناءً على العوامل التي ذكرناها بالتفصيل سابقا.
يمكن التعبير رياضيًا عن عزم القصور الذاتي في ابسط صوره من خلال المعادلة التالية:
I = m × r2
حيث:
- I ترمز لعزم القصور الذاتي
- m هي كتلة الجسم
- r2 هو مربع المسافة العمودية عن محور الدوران
- يقاس عزم القصور الذاتي بوحدة كيلوجرام في متر مربع (Kg.m2 )
يمكن حساب عزم القصور الذاتي لنظام مركب من خلال المعادلة التالية:
I = ∑m × r2
حيث:
- I ترمز لعزم القصور الذاتي
- ∑m ترمز لمجموع الكتل
- r2 ترمز الى مجموع مربع المسافة العمودية عن محور الدوران
أي يمكننا الحصول على عزم القصور للنظام المركب من خلال جمع عزوم القصور الذاتي لأنظمته الفرعية المكونة له، بشرط أن تتحرك جميعها حول نفس المحور، وقد تكون هذه الأنظمة الفرعية جسيمات أو جزئيات، ويفضل البدء بقياس المسافة للجسيم في النظام المركب عن المحور ثم تربيعها، ومن ثم ضرب قيمة التربيع في كتلة هذا الجسيم، ثم تكرار العملية الحسابية لكل جسيم في النظام المركب وجمع القيم كاملةً بعد ذلك.
قم بزيارة معمل العلوم الافتراضي وأكتشف عالم من العلوم بين يديك!
أطلب ديمو مجاني الآن! لتعش تجربة المعامل الإفتراضية
عزم القصور الذاتي للأشكال الهندسية (معادلات القصور الذاتي)
كما وضحنا سابقًا، يمكن حساب عزم القصور لأي جسم له شكل يمكن وصفه بواسطة صيغة رياضية عادةً عن طريق حساب التفاضل والتكامل لهذا الجسم.
وكما وضحنا من قبل الصيغ الرياضية للتعامل مع عزم القصور الذاتى: القانون ((البسيط)) الذى يحدد عزم القصور الذاتى هو I=MR^2 ،، حيث الـ R فتمثل آخر نقاط الجسم عن مركز الثقل وغالباً ما تمثل نصف قطر الأشكال الدورانية وطول الأشكال المستقيمة ..
وهناك قانون أعم وأشمل لحساب عزم القصور والذى يُلجأ إليه لحساب الأشكال الغربية والغير منتظمة، حيث يتم حسابه بأستخدام التكامل العادى أو الثنائى (( للأشكال ذات البعدين )) أما الأشكال الثلاثية الأبعاد فيتم أستخدام التكامل الثلاثى معها.
سنعرض فيما يلي قائمة بالصيغ الخاصة بعزم القصور للأشكال المختلفة:
عزم القصور الذاتي للاسطوانة (المجوفة)
يتم حسابه من خلال المعادلة التالية:
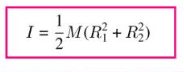
عزم القصور الذاتي للمستطيل
يتم حسابه من خلال المعادلة التالية:

عزم القصور الذاتي للقرص
يتم حسابه من خلال المعادلة التالية:
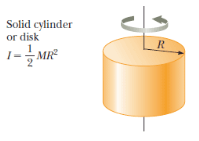
عزم القصور الذاتي لكرة صلبة
يتم حسابه من خلال المعادلة التالية:
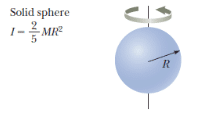
عزم القصور الذاتي للقضيب (الرفيع)
يتم حسابه من خلال المعادلة التالية:

عزم القصور الذاتي للمثلث
أولاً: عزم القصور الذاتي للمثلث
بالنسبة للمحور الذي يمر عبر النقطة الوسطى بالتوازي مع قاعدته
يمكن التعبير عنه من خلال المعادلة التالية:
I = bh3 / 36
حيث:
- b هو عرض القاعدة ، وتحديداً جانب المثلث الموازي للمحور
- h هو ارتفاع المثلث (عمودي على المحور والقاعدة).
ثانياً: عزم القصور الذاتي للمثلث
بالنسبة لمحور يمر عبر قاعدته
يمكن التعبير عنه من خلال المعادلة التالية:
I = bh3 / 12
ثالثاً: عزم القصور الذاتي للمثلث
بالنسبة لمحور يمر عمودي على قاعدته
يمكن التعبير عنه من خلال المعادلة التالية:
Iy’ = (hb / 36) (b2 – b1 b + b12)
توضيح المعادلة السابقة:
في حالة ايجاد عزم القصور للمثلث و يكون محوره عموديًا على قاعدته، علينا أولاً أن نأخذ في الاعتبار أن المحور y’-y ‘يستخدم في تقسيم المثلث بأكمله إلى مثلثين A و B كلاً منهم قائم الزاوية. ومع ذلك، سيكون لهذه المثلثات قاعدة مشتركة تساوي h ، والارتفاعات b1 و b2. وبالتالي يكون عزم القصور الذاتي لكليهما:
Iy ‘= hb13 / 12 + hb23 / 12
وإذا أخذنا في الاعتبار أن b2 = b – b1 حيث يكون المحور الموازي y-y عبر النقطه الوسطى على مسافة ⅔ (b / 2 – b1) من y’ y ‘، فيمكننا بسهولة إيجاد أو حساب عزم القصور. يمكننا استخدام نظرية المحور المتوازي لفعل ذلك. ومن ثم، بعد الاستبدالات الجبرية نحصل على التعبير على النحو التالي:
Iy’ = (hb / 36) (b2 – b1 b + b12)
ملحوظة:
نظرية المحاور المتوازية هي من النظريات المهمة في قوانين الفيزياء والرياضيات، والتي تسمح لنا بحساب قيمة عزم القصور للجسم عند أي محور ما عدا مركز الثقل، ويعبر عنها رياضياً كالتالي:
Idisplacd= Icenter+MR^2
حيث أن:
- Icenter هي عزم القصور الذاتي عند مركز الثقل
- Idisplaced تمثل قيمة العزم الجديد عند المحور الجديد المراد حسابه
- R هي المسافة بين مركز الثقل للجسم وبين المحور الجديد.
عزم القصور الذاتي الدوراني
عندما يتم تطبيق عزم على جسم ما، فإنه يبدأ في الدوران مع تسارع يتناسب عكسًا مع لحظة قصوره الذاتي. يمكن اعتبار هذه العلاقة بمثابة قانون نيوتن الثاني للدوران. لحظة القصور الذاتي هي كتلة الدوران وعزم الدوران هو قوة الدوران.
يمكننا حساب الطاقة الحركية الدورانية من خلال القانون التالي:
الطاقة الحركية الدورانية= عزم القصور الذاتي × مربع السرعة الزاوية
الفرق بين عزم القصور الذاتي وعزم الدوران
لنعرف الفرق بينهم يجب علينا أولا ان نوضح مفهزم كلا من التسارع الزاوي، وعزم الدوران، والقصور الذاتي الدوراني:
- التسارع الزاوي: معدل تغير السرعة الزاوية، وغالبًا ما يتم تمثيله بواسطة α.
- عزم الدوران: تأثير الدوران أو الالتواء للقوة.
- القصور الذاتي الدوراني: ميل الجسم الدوار للبقاء في حالة دوران ما لم يتم تطبيق عزم عليه.
يمكننا تعريف عزم الدوران الآن على أنه القوة التي تُطبق أو تؤثر على جسم ما وتؤدي إلى تحريكه دورانيًا بتسارع يتناسب عكسيًا مع قصوره الذاتي، لذلك يمكننا القول أن عزم الدوران في الحركة الدورانية كالقوة في الحركة الخطية.
يمكن توضيح العلاقة بين عزم الدوران وعزم القصور الذاتي من خلال المعادلة التالية:
عزم الدوران = عزم القصور الذاتي × التسارع الزاوي
τ = I × α
حيث:
- τ هو عزم الدوران (القدرة التي تُمكن الجسم من الدوران)، ويقاس بوحدة نيوتن.م .
- I عزم القصور الذاتي، ويقاس بوحدة كجم.م2.
- α هو التسارع الزاوي (الذي يُعبر عن معدل تغير السرعة الزاوية)، ويقاس بوحدة م/ث2.
تخضع الحركة الدائرية أو الدورانية لقانون نيوتن الأول، وبالتالي يخضع عزم القصور لنفس القانون عندما يحاول المحافظة على حالة دوران جسم ما دون أن يؤثر عليه عزم دوران آخر، بينما عزم الدوران هو بمثابة قانون نيوتن الثاني للدوران؛ اذا اعتبرنا أن عزم القصور أنه كتلة الدوران في قانون نيوتن وعزم الدوران أنه قوة الدوران في قانون نيوتن.
ايجاد عزم القصور الذاتي بطريقة بفلر
تستخدم طريقة التعليق بفلر لايجاد عزم القصور الذاتي عملياً لقضيب معدني حول محور عمودي على طوله و يمر من مركز ثقله (منتصفه) بواسطة تعليقه بخطين متوازيين و متساويين بالطول و موازيين الى هذا المحور (محور الدوران).
فعند تعلق قضيب معدني كتلته (m) وطوله (l) وعزم قصوره الذاتي حول محور عمودي على طوله و مار من منتصفه هو (I) بخيطين متساويين بالطول ومتوازيين مثل(AC)، ( BD) وكان طول كل من الخيطين (L) والمسافة بينهما (d) بحيث يكون القضيب افقيا فأن الشد في كل من الخيطين سيكون مساويا الى (1/2mg) حيث g هي العجلة الارضية، فلو ازيح القضيب افقيا من الموضع (CD) إلى الموضع الجديد بزاوية صغيرة ، فان كل من خيطي التعليق يميل بزاوية (Φ)
عزم القصور الذاتي وتطبيقاته
يمكننا ملاحظة عزم القصور في أمثلة كثيرة في الحياة العملية أو اليومية فمثلا:
- عندما تركب أي نوع من المركبات ، إذا تحركت للأمام بشكل غير متوقع ، يمكن أن تشعر برجة للخلف. فمثلا عندمل يركب شخص ما حافلة وتتحرك ثم تتوقف مرة خرى لاي سبب تعاود التحرك، سيلاحظ حينها تحرك الجزء العلوي من جسده للأمام، بينما الجزء السفلي من جسده يبقى ثابتًا، وهذا بسبب عزم القصور، فالجزء السفلي من جسده مرتبط مع الحافلة فعندما توقفت الحافلة توقف معها الجزء السفلي، بينما الجزء العلوي منفصل عن الحافلة فعند توقفها؛ يبدأ بمقاومة حالته الحركية عن طريق التحرك نحو الأمام.

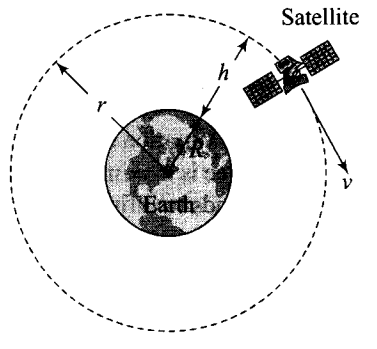
- الأقمار الصناعية في الفضاء تعتبر مثال جيد على القصور الذاتي في الفضاء، حيث أنها تدور حول جسم أكبر منها بكثير، وتستمر هذه الأقمار بالحركة دون توقف؛ ذلك بسبب تطبيق القصور الذاتي للحركة عليها، مما يجعلها تتحرك في حركة دائرية مستمرة.
- إيقاف العربة بشكل مفاجئ يؤدي إلى سقوط الأشياء الموجودة في أعلاها.
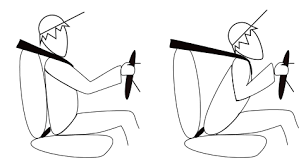
- عند وضع حزام الأمان وتغيير سرعة السيارة بشكل مفاجئ؛ ستزيد قوة شد حزام الأمان.
- ستنتقل المعدات المتوفرة في منزلك من مكان إلى آخر عندما تتحرك ، أو ستبقى في نفس الأماكن. هذا بسبب تأثير المقاومة لمقاومة التغيير من خلال الخضوع للحركة أو البقاء في نفس الحالة.
- عندما يضاف سكر أو ملح إلى كوب من الماء، ثم يُحرك بواسطة ملعقة بشكل دائري، نلاحظ أن المياة تستمر بالدوران حتى بعد إزالة الملعقة من الكأس، والسبب في ذلك يعود إلى عزم القصور الذي يحافظ على حركة المياة دون توقف لبعض الوقت.

- تكون أقطار العجلات أكبر في السيارات الكبيرة والشاحنات؛ وذلك للحصول على عزم أكبر.
تقدم براكسيلابس معامل العلوم الافتراضية التي تمكنك من إجراء مجموعة تجارب افتراضية معملية في مختلف فروع الفيزياء
 براكسيلابس المدونة العربية لمعامل العلوم الإفتراضية براكسيلابس
براكسيلابس المدونة العربية لمعامل العلوم الإفتراضية براكسيلابس