Last Updated on August 22, 2025 by Muhamed Elmesery
One of the most famous and revolutionary scientific theories of the 20th century is Einstein’s theory of relativity. It was proposed by the German-born physicist, Albert Einstein, in 1905 and has since then been accepted as a fundamental theory of physics. This theory has brought about a radical transformation in the way we understand the universe and has had a profound impact on many fields such as cosmology, astrophysics, and quantum mechanics.
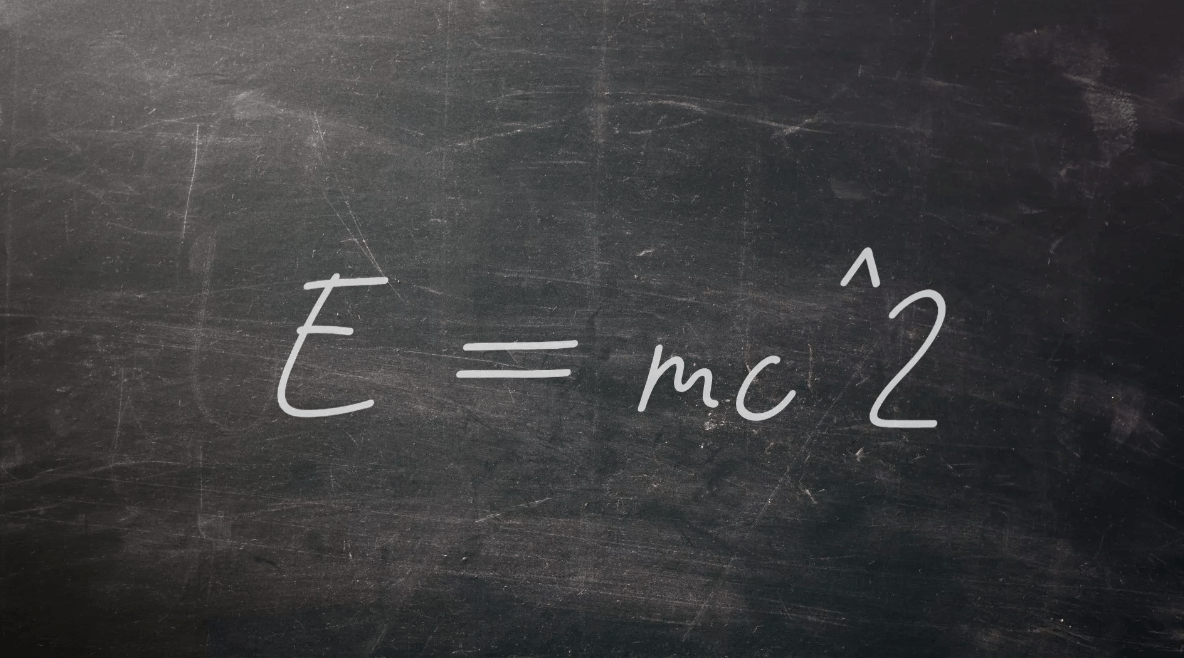
In this article, we will take a closer look at Einstein’s theory of relativity, explore how it works, what its aspects of applications are, and how it changed the way we view the universe.
Table of Contents
Introduction to Einstein’s Theory of Relativity
Einstein’s theory of relativity is a groundbreaking concept that explains how gravity influences the movement of objects. It states that:
“All observers, regardless of their own movement, must abide by the same physical laws and that the speed of light is always the same, regardless of the motion of its source.”
This theory is considered to be one of the most significant scientific breakthroughs of the 20th century and has had a profound impact on our comprehension of the cosmos.
At its foundation, the theory suggests that space and time are not absolute, but instead are relative to the motion of the observer. This implies that all observers in any given reference frame must adhere to the same physical laws, no matter their motion. This theory also introduced the idea of curved spacetime, which is the concept that space and time can be altered and curved by the presence of both matter and energy.
The concept of relativity is divided into two distinct parts:
- The general theory of relativity.
- The special theory of relativity.
The general Einstein’s theory of relativity is concerned with investigating gravity and the way it influences the movement of matter in the cosmos. The special theory of relativity focuses on the velocity of light and how it is altered due to motion.
The Principle of Relativity
The Principle of relativity is a fundamental tenet of Einstein’s relativity. It states that:
“The laws of physics are the same for all observers regardless of their motion.”
Accordingly, the results of any experiment conducted in one frame of reference will be identical for all observers, regardless of their motion. This axiom is based on the notion that the speed of light is invariable for each observer, regardless of their motion in relation to the source.
In other words, if two observers were to measure the speed of light from a distant star, they would both measure the same value, irrespective of their motion relative to the star. This is a significant notion in Einstein’s theory since it permits us to compare experiments done in distinct frames of reference and draw logical conclusions and inferences.
More on Reference Frames and Relative Motion
A reference frame serves a critical purpose in the realm of relativity. It is an observational standpoint in space that is not experiencing any motion (acceleration), from which a position can be determined across 3 dimensions (i.e. stationary or unchanging velocity). Not only that, a reference frame is able to ascertain measurements of the timing of events using a reference device that has consistent periodicity.
An event is a moment which can be identified with respect to a reference frame, and it is known as a “point” in spacetime. Despite the fact that light requires time to reach the clock after an event has taken place, relativity theory states that the speed of light is constant in all reference frames, so that light pulses can be used to accurately measure distances and determine the time at which the event occurred.
As an illustration, the detonation of a firecracker can be categorized as an “event”. We can completely identify an event by its four spacetime coordinates: the time of occurrence and its 3-dimensional spatial site make up a reference point. We may refer to this as reference frame (S).
In Einstein’s theory of relativity, we often need to determine the coordinates of an event from different reference frames. The equations that link measurements taken in various frames are referred to as transformation equations.
Standard Configuration
To understand how spacetime coordinates are perceived by observers in different reference frames, it is beneficial to employ a simplified setting with frames in a standard configuration. This makes it possible to simplify the mathematics involved while still reaching the same conclusions.
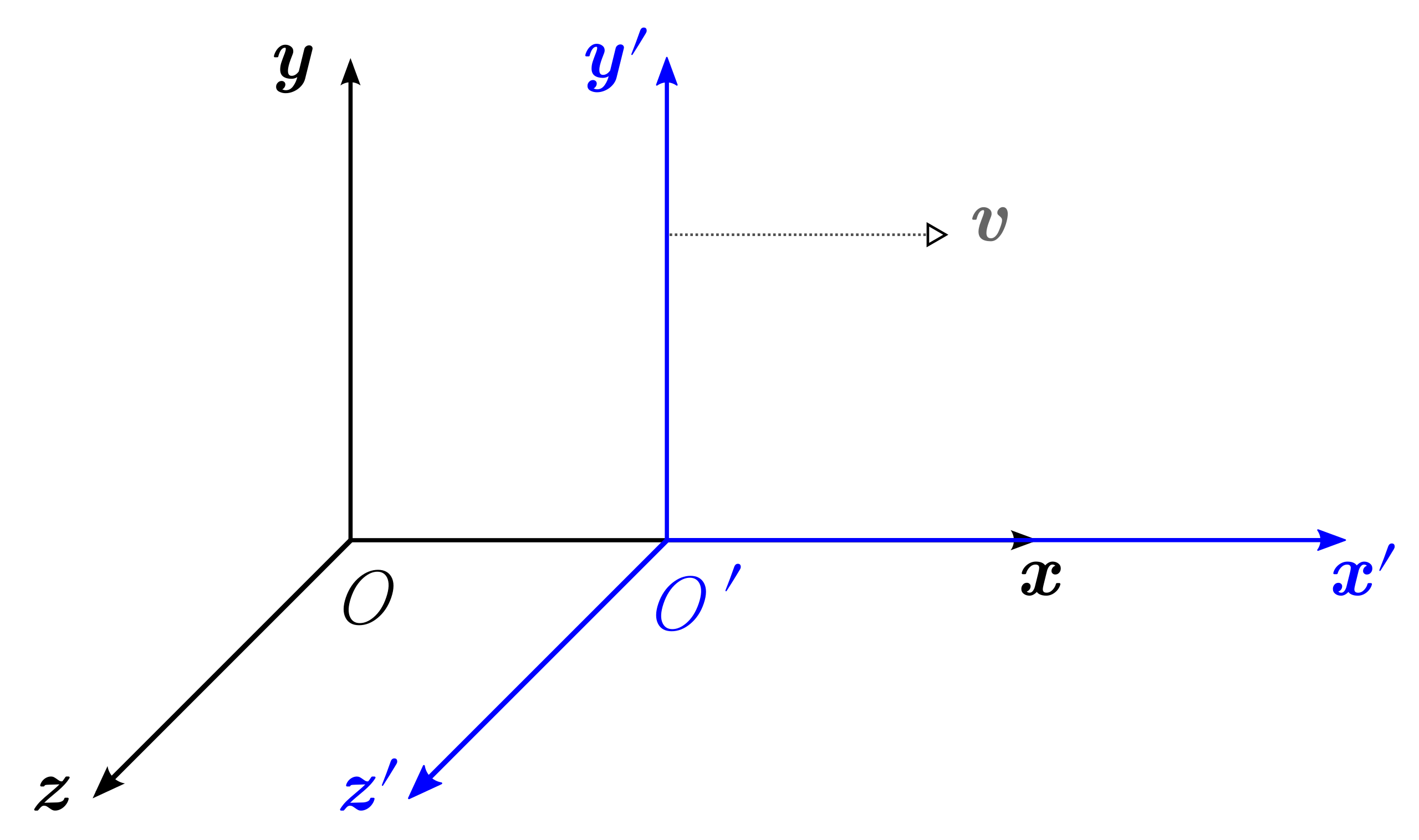
The figure shows two Galilean frames of reference (i.e. classical 3-space frames) in relative motion. The one labeled S is owned by the first observer O, while S′ belongs to the second observer O′.
- The x, y, and z axes of frame S are parallel to the appropriate primed axes of frame S’.
- Frame S’ moves in a single direction, namely the x-direction of frame S, with a steady velocity (v) as measured in frame S.
- The origins of frames S and S’ coincide when the time t = 0 in frame S and t’ = 0 in frame S’.
In Einstein’s theory of relativity, there is no absolute reference frame, making the concept of ‘moving’ relative as everything could be moving with respect to some other frame. Consequently, two frames that move together at the same speed in the same direction are known as co-moving. In this context, S and S′ are not co-moving.
Deficiency of Finding an Absolute Time Frame
Galileo was the first to propose the idea of the principle of relativity, which claims that physical principles are the same in all inertial frames of reference, and this concept was embraced by Newtonian physics. During the late 19th century, the detection of electromagnetic waves prompted some physicists to propose that the universe was filled with a material they termed “aether”, which supposedly served as the medium transmitting these vibrations (similar to the way sound is passed through the air).
This aether was assumed to be an absolute frame of reference for measuring velocities, and it was thought to be still and stationary relative to the Earth or any other fixed point of reference. It was thought that the aether was sufficiently flexible to carry electromagnetic waves, and could interact with matter, but would not obstruct any objects passing through it (the sole quality of the aether was that it permitted electromagnetic waves to travel).
The findings of various experiments, such as the Michelson–Morley experiment in 1887 (which have since been confirmed with more precise and modern experiments), caused the theory of special relativity to be developed, since it indicated that the aether did not exist. Einstein then eliminated the concept of an aether and the absolute state of rest.
According to relativity, any reference frame that is in constant motion will identify the same physical laws. Notably, the speed of light in a vacuum will always be measured as c, regardless of the speed of the system that is measuring it.
If We Excluded Relativity’s Second Postulate
Starting from the “Principle of Relativity”, without bringing in the second postulate, one can demonstrate that the space-time transformations between inertial frames are either Euclidean, Galilean, or Lorentzian. Furthermore, the Lorentzian case brings forth the conservation of relativistic intervals as well as a definite upper limit for speed (i.e. a certain limited speed). Observations seem to indicate that this speed is the speed of light in a vacuum.
Exploring the Special Theory of Relativity
In 1905, Albert Einstein published an article known as “On the Electrodynamics of Moving Bodies” which unveiled his theory of special relativity. This followed after experiments such as the Michelson-Morley null result indicated that the luminiferous aether, a hypothesis of the time, was not present.
Try PraxiLabs 3D Science Experiments variety and start your virtual learning experience!
This eventually led Einstein to develop special relativity to handle all movement, especially those at velocities near the speed of light (relativistic velocities). Currently, it is substantially accurate when gravitational and quantum effects are insignificant. Nonetheless, the Newtonian model is still applicable for everyday motions at low velocities compared to the speed of light.
The special Einstein’s theory of relativity is based on the idea that the speed of light is always the same regardless of the motion of its source. One of the postulates states that:
“The speed of light is the same for all observers regardless of their motion.”
The theory explains how the laws of physics are affected by motion. This is stated clearly in its second postulate:
“Time passes differently for two observers depending on their motion relative to one another.”
For example, if two observers were moving at different speeds relative to one another, the observer who is moving faster would experience time as passing more slowly than the observer who is moving slower. The phenomenon is known as time dilation.
The Special Theory of Relativity also explains the phenomenon of length contraction. This is the idea that the length of an object appears shorter to an observer who is moving relative to it. This is due to the fact that the speed of light is always the same regardless of the motion of its source.
Numerous experiments have supported the varied implications of special relativity, such as the relativity of simultaneity, length contraction, time dilation, the relativistic velocity addition formula, the relativistic Doppler effect, relativistic mass, a universal speed limit, mass–energy equivalence, the speed of causality, and the Thomas precession.
It has replaced the traditional idea of a universal time with one dependent on the reference frame and spatial location. Instead of a constant time interval between two occurrences, there is an invariant spacetime interval. In conjunction with other physical laws, the two postulates of special relativity predict the equivalence of mass and energy as expressed in the equation E = mc2, where c is the speed of light in a vacuum. This theory also clarifies the relationship between electricity and magnetism.
This theory has been foundational for many of the most important scientific discoveries of the past century. Among these discoveries is the realization that time is not absolute, as previously thought, but instead is relative to the observer’s velocity. By which we were led to a better understanding of the structure of the universe, and has helped us better understand the behavior of particles at the subatomic level.
Additionally, the special theory of relativity has helped to explain phenomena like gravitational waves, and the expansion of the universe. It has also been used to develop technologies such as GPS and particle accelerators. This theory continues to be an invaluable tool for scientists, and its discoveries have helped us to unlock the mysteries of the universe.
Understanding the General Theory of Relativity
The general theory of relativity, or the general theory of gravity, is a theory developed by Albert Einstein between 1907-1915. It explains the behavior of gravity and how it affects the motion of objects in the universe. This theory states that:
“matter and energy can distort space and time, and this distortion affects the motion of objects.”
The general Einstein’s theory of relativity is based on the idea of curved spacetime. This is the idea that space and time can be bent by the presence of matter and energy. Which means that the path of an object in space can be curved by the presence of other objects with mass.
The general theory of relativity also introduced the concept of black holes, which are regions of space where the gravitational pull is so strong that nothing, not even light, can escape from them.
Analyzing the Equation of Einstein’s Theory of Relativity
Einstein’s theory of relativity is expressed in a mathematical equation known as Einstein’s Field Equation. This equation relates the curvature of spacetime to the energy and momentum of matter and energy. It states that:
“The curvature of spacetime is directly proportional to the energy and momentum of matter and energy.”
The equation is written as follows:
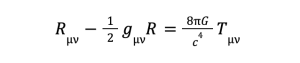
Where
- Rμν: the Ricci curvature tensor.
- gμν: the metric tensor.
- R: the Ricci scalar.
- G: the gravitational constant.
- c: the speed of light.
- Tμν: the stress-energy tensor.
The equation was derived by Einstein in 1915 and is considered to be one of the most important equations in physics. It is used to explain the behavior of gravity and is the basis for general Einstein’s theory of relativity.
Exploring the Concept of Time Dilation
The concept of time dilation is a key part of the special theory of relativity. It states that:
”The passage of time can vary depending on the motion of the observer.”
This means that if two observers are moving relative to one another, the observer who is moving faster will experience time as passing more slowly than the observer who is moving slower.
This phenomenon can be demonstrated using the famous “Twin Paradox“. In this thought experiment, two twins are separated and one of them travels at a speed close to the speed of light for a significant amount of time. When the twin returns, it is found that the twin who stayed still has aged more than the one who traveled.
This is because the twin who traveled experienced time as passing more slowly due to his motion relative to the one who stayed still. Time dilation has been confirmed in experiments and is an important part of the special theory of relativity.
Examining the Impact of Einstein’s Theory of Relativity
Einstein’s theory of relativity has had a remarkable influence on our comprehension of the cosmos. It has completely reshaped our perspectives on space and time and has had a noteworthy consequence on various disciplines such as astrophysics, cosmology, and quantum mechanics.
For example, the general theory of relativity explains the behavior of gravity, which has allowed us to better understand the structure of the universe. It has also been used to explain the phenomenon of gravitational lensing, which is the bending of light due to the presence of matter and energy.
The special theory of relativity has also been used to explain the phenomenon of time dilation and has had a major impact on our understanding of the nature of time. It has also been used to explain the behavior of matter and energy at the quantum level, which has led to the development of quantum mechanics.
Exploring the Applications of Einstein’s Theory of Relativity
Einstein’s theory of relativity has many practical applications. For example, it is used to explain the behavior of GPS systems, which rely on the accurate measurement of time in order to calculate the user’s position. GPS systems use the effects of time dilation to correct for the effects of the user’s motion relative to the satellite.
The theory is also used in the study of black holes. Black holes are regions of space where the gravitational pull is so strong that not even light can escape from them. This phenomenon is explained by the general theory of relativity, which states that matter and energy can distort space and time.
The theory is also used in the study of cosmology, the study of the structure and evolution of the universe. The general theory of relativity explains the behavior of the universe on large scales and is used to calculate the age, size, and shape of the universe.
Debates Surrounding Einstein’s Theory of Relativity
Einstein’s theory of relativity, formulated by Albert Einstein, is a prominent and transformative scientific contribution of the 20th century. It has been the focus of much debate and challenge, particularly due to its inability to account for the effects of gravity on minuscule scales.
The theory has also been criticized for its lack of simplicity. The equations of the theory are complex and require a significant amount of mathematical knowledge in order to be understood. This has led to some debates about whether or not the theory is truly a valid scientific theory.
All in all, the theory has been criticized for its lack of experimental evidence. The equations of the theory have only been tested on very large scales, and there has been no experimental evidence to support its predictions on smaller scales.
Join PraxiLabs virtual physics lab for FREE and enjoy knowing more about Einstein’s theory!
 PraxiLabs A virtual world of science
PraxiLabs A virtual world of science






