Last Updated on May 15, 2025 by Muhamed Elmesery
Pressure is an intrinsic property of matter. You can exert pressure on a solid, a liquid, or on a gas, and so can solids, liquids, and gasses according to the surrounding conditions. A famous example in this context is the cautionary signs on your perfume bottle, saying “the bottle should not be left in the sun, or in high temperatures, to avoid explosions.”
Liquids and gasses—known as fluids—are the two types of matter that go through continuous and noticeable changes caused by pressure. Many laws of physics discuss and explain the behavior and mechanisms of fluids. And Pascal’s law is on the top of this list. The law is also known as the principle of transmission of fluid-pressure, or Pascal’s principle.
Discover everything about Pascal’s law definition, its formula, and applications in this article. Besides, we are going to see how Pascal’s law is used in hydraulic lift and how to calculate Pascal’s law. Let’s start figuring this law out…
Discover Praxilabs Virtual Physics Lab
Table of Contents
Pascal’s Law of Hydrostatics
The French mathematician, philosopher, and physicist Blaise Pascal was interested in developing the concept of pressure (1623-1662). He discovered his famous Pascal’s law while conducting an interesting experiment. In addition to his interest in pressure, Pascal was the scientist who developed the modern theory of probability.
The experiment consisted of a 10 m vertically inserted long pole into a barrel. The barrel was filled with water, and a water flow was running through that long pole. As the water was poured, he noticed that the barrel burst due to the water’s pressure. He concluded that the pressure caused by the water—or any fluid in general—was transmitted through the water in all directions.

Pascal realized that, for a static fluid, the pressure at a point will be the same across all planes passing through that specific point of the fluid. For example, if you are using static oil instead of water, and you are conducting the same experiment as Pascal did, the final result will be the same. Such that:
The oil going through the tube will cause the barrel to burst. Hence, the pressure caused by it will be transmitted to the oil in the barrel and in all directions.
In itself, the term fluid statics—also known as hydrostatics—is a branch of fluid mechanics that is concerned with studying the equilibrium condition of a floating body and a submerged body. In other words, it studies fluids at hydrostatic equilibrium and the pressure in a fluid, or exerted by a fluid, on any immersed body.
Fluid statics is very contrary to fluid dynamics, since the first studies the conditions under which fluid are at rest and are in a stable equilibrium, whereas the latter refers to studying fluids that are in motion. Nevertheless, hydrostatics is a subcategory of fluid statics.
Hydrostatics is fundamental to hydraulics. Hydrostatics is relevant to both astrophysics (in understanding the anomalies of earth’s gravitational field) and geophysics (in understanding plate tectonics), while it is also important to many other fields, such as meteorology and medicine (in the context of blood pressure).
Why do oil and wood float on the water’s surface?
Why does atmospheric pressure change with altitude?
Why is still water’s surface always level according to the earth’s curvature?
The answer to these three previous questions is hydrostatics as many phenomena in our daily life can be elaborately explained using this term, and how it functions and works. Thus, Pascal’s law of hydrostatics helps us justify and understand many of the questions around us.
Intermolecular Forces and Pascal’s Law
One thing to note is that Pascal’s law is not applicable on gasses. And it is only used with liquids… Can you guess the reason behind this?
All types of matter are composed of particles at the microscopic level, where these particles are in random motion all the time. In the solid state of matter, particles are strongly bound together, where their motion is restricted to only jiggle about virtual and fixed equilibrium positions relative to each other. Because of this, we consider solids to be rigid.
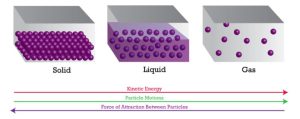
On the other hand, gas particles interact briefly under certain circumstances, and they cause intense collisions with other gas’ particles or with the container’s walls. Liquids stand alone in the middle between solids and gasses, where the motion of particles in a liquid is random but not as chaotic as that of the gas.
The average attractive forces between the particles of a liquid are sufficient to make the liquid cohesive yet are weak enough to allow the liquid to flow. Liquid particles pass each other smoothly while flowing, without causing the liquid’s mass to undergo any macroscopic separation.
Create an account to try our virtual experiment for FREE
Pascal’s Law Formula
Now, can you deduce Pascal’s law formula based on what we discussed previously?
Pascal’s law formula tackles three quantities of physics, which are:
- Pressure, denoted as P.
- Force, denoted by F.
- Area (or surface area), and it is denoted by A.
And the law is stated as follows:
F = p*A
whereas the formula of hydrostatic pressure is given as
Δp = g(Δh)
where
Δp: the hydrostatic pressure exerted by the liquid, measured in (N.m-2, or Pa),
ρ: the density of the liquid, measured in (kg.m-3),
g: the acceleration due to gravity, put as 9.81 m.s-2, and
Δh: the difference in height of the fluid column, given in (m).
According to Pascal’s law, the change in pressure of a fluid at rest and in a closed container is transmitted undiminished and without any loss to every part of the fluid, as well as to the walls of the container.
Check Your Understanding!
Check the figure below and ask yourself: which pressure will give the highest value of the three readings?
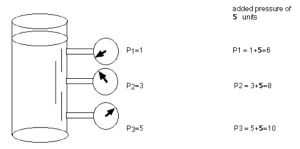
The right answer to this question is P3. The reason that P3 has the highest value between the other two readings is because it has the highest level of fluid above it.
If the container undergoes an increase in overall pressure, this pressure will affect all the gauges equally. To comprehend this example more, suppose that our initial readings were 1, 3, and 5 units of pressure for P1, P2, and P3, respectively. We will add 5 more units of pressure to the system; thus the new readings will be 6, 8, and 10 for P1, P2, and P3, respectively.
State and Prove Pascal’s Law
Pascal’s principle, or Pascal’s law, can be defined and stated in three different statements, which are:
“A change in pressure at any point in an enclosed fluid at rest is transmitted undiminished to all points in the fluid”
or
“Pressure exerted on a fluid in an enclosed container is transmitted equally and undiminished to all parts of the container and acts at right angle to the enclosing walls”
and
“The pressure applied to any part of the enclosed liquid will be transmitted equally in all directions through the liquid.”
Since Pascal was a mathematician, his law can be mathematically proved without any doubts. If you are a student, the derivation of Pascal’s law is a very common question that you will encounter during your physics or engineering study.
You might be wondering what is the point of deriving or proving physics laws mathematically, right?
The thing is mathematical derivations and proofs will help you understand further details regarding the law you are tackling or working with. In addition to its significant help in memorizing the laws more clearly, it also develops your skillset over time, especially when it comes to solving more complicated problems and questions. Thus, in this section, Pascal’s law will be proved mathematically… Let’s start!
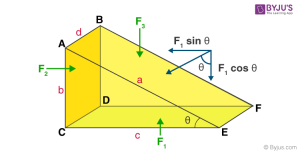
Consider an arbitrary prismatic right-angled triangle, put in a liquid of density rho (). The prismatic triangle is very small. Thus we consider every point of it to be at the same depth as that of the liquid’s surface. As a consequence, temperature (T) is the same at all these points, as well as the effect of gravity.
In the triangle:
- Let ad, bd, and cd be the area of the faces ABFE, ABDC, and CDFE, respectively.
- Let P1, P2, and P3 be the pressure on the faces ABFE, ABDC, and CDFE, respectively.
Since pressure exerts a normal force to the surface, let P1 exert force F1 on the surface ABFE, P2 exert force F2 on the surface ABDC, and P3 exert force F3 on the surface CDFE.
The forces F1, F2, and F3 are hence given by
F1 = P1 × area of ABFE = (P1)*(ad)
F2 = P2 × area of ABDC = (P2)*(bd)
F3 = P3 × area of CDFE = (P3)*(cd)
Note: the net force acting on the prism will be equal to zero, as long as the prism is in equilibrium.
Thus,
F1 sin(θ) = F2, and
F2 cos(θ) = F3
Consequently,
(P1)*(ad) = (P2)*(bd)
(P1)*(ad) = (P3)*(cd)
From #1 and #2, we realize that
P1 = P2 and P1 = P3
∴ P1 = P2 = P3
This last equation shows that all the definitions of Pascal’s law are proved right and they follow a well-constructed mathematical logic.
Request a Demo To Start The Virtual Labs Experience
How to Calculate Pascal’s Law?
In the previous pages, you were introduced to all the needed information and tools you need to know about Pascal’s law; from the law’s history and how it works to the mathematical derivation and the different formulas of it. At this point, you are now ready to know how to really calculate and account for Pascal’s law.
To not waste your time, we will straightforwardly show two problems and walk through their solution.
- Calculate the pressure acting on the water at a depth of 1 m at 4°C?
Solution
The depth of the water column = 1 m
The density of water at 4°C = 1000 kg/m3
The formula in use is
p = ρgh
Thus,
p = (1000 kg/m3)(9.81 m.s-2)(1 m) = 9810 Pa
- Consider the automobile hydraulic system shown in the figure below, where a force of 100 N is applied to the brake pedal, which acts on the pedal cylinder through a lever.
A force of 500 N is exerted on the pedal cylinder. Pressure created in the pedal cylinder is transmitted to four wheel cylinders. The pedal cylinder has a diameter of 0.500 cm, and each wheel cylinder has a diameter of 2.50 cm.
Calculate the force F2 created at each of the wheel cylinders.
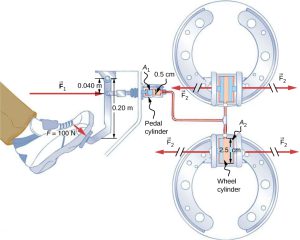
Solution Strategy
The cross-sectional areas A1 and A2 can be calculated from their given diameters. Since the force F1 that is applied to the pedal cylinder is given, the law F1*A1 = F2*A2 can be used to find the force F2. By manipulating the equations algebraically, we can deduce the value of F2 through substitution with the values.
Solution
Pascal’s principle applied to hydraulic systems is given by
F1 * A1 = F2 * A2
Thus,
F2 = (A2/A1)*F1 = ((π (r2)2) / (π (r1)2)) * F1
F2 = ((1.25 cm)2 / (0.250 cm)2) × 500 N
F2 = 1.25 × 104 N
Discussion
This value (1.25 × 104 N) is the amount of force exerted by each of the four wheel cylinders. Note that if we added more wheels and each has a 2.50 cm diameter, each will exert the same amount of force.
Applications of Pascal’s Law
A virtual lab can be of a great help to you! Where the finely-created experiments and 3D simulations will guide you through the topics of your interest, only with a click. PraxiLabs offer you many experiments to apply Pascal’s law by yourself, and tackle many of the pressure’s problems.
 PraxiLabs A virtual world of science
PraxiLabs A virtual world of science





