Learn How to Determine the Coefficient of Viscosity Using Stoke’s Method

Last Updated on August 29, 2023 by Nourhan Essam

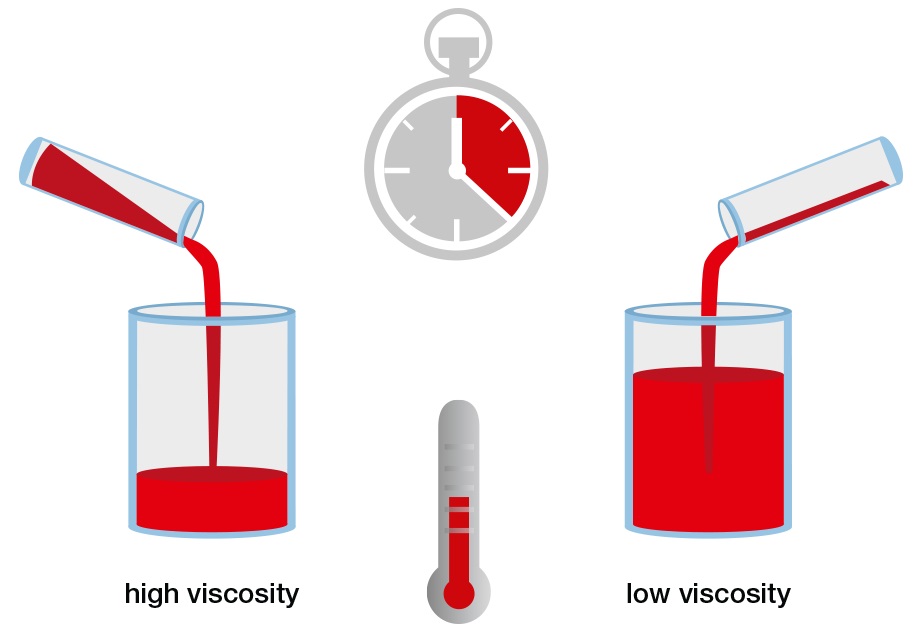
Imagine that you have a cup with a hole in the bottom. If you pour honey or glycerin into the cup, you will find that the cup drains very slowly. But in the case of water, the cup will drain much more quickly. That happens because “viscosity” is higher in the case of honey or glycerin when compared to other liquids’ viscosities.

Viscosity is one of the essential parameters that describe the physicochemical properties of liquids. It is a measurement of a fluid’s resistance to flow or change in shape at a given rate

In this article, we will discuss what is meant by viscosity, the concept of coefficient viscosity, how to determine the coefficient of viscosity using Stoke’s method, and more.

What is Viscosity?

Viscosity can be defined as a force multiplied by a time divided by an area. It is a measure of a fluid’s resistance to flow and describes the internal friction of a fluid that is moving.

For further understanding, when you put some drops of honey on one side on an inclined surface and some water droplets on the other side and observe the flow of fluid. You will notice that water flows much faster than honey, which flows very slowly and cannot be moved easily. This happens due to the viscosity of the material.

Notice that a high viscosity of fluid resists motion because its molecular makeup gives it a variety of internal friction. However, the low-viscosity fluid flows easily because its molecular makeup results in little or no friction in case of movement.

Gases have viscosity like fluids but it is difficult to be noticed in ordinary circumstances.

Viscosity depends on factors related to the fluid’s state, such as:

•         The fluid temperature
•         Deformation rate
•         pressure

Note: The dependence on these factors may be negligible in certain cases. For example, the Newtonian fluid’s viscosity does not vary with the deformation rate.

Coefficient of Viscosity

To understand what is meant by the coefficient of viscosity, you should understand the meaning of “The viscous gradient” first.

Viscous Gradient

The viscous gradient is the distinction inside the velocity among the fluid’s adjacent layers If more force is applied by the upper layer to move forward the more will be the viscous gradient.

The viscous gradient is the difference in the velocity between the fluid’s adjacent layers. If more force is applied by the upper layer to move forward.

 It is given by v/x, where v is the velocity difference and x is the difference of distance between the two layers.

Now, let’s define the coefficient of viscosity:

The coefficient of viscosity is the ratio of the shearing stress to the velocity gradient of the fluid (η).

The coefficient of viscosity is given by the following relation:

        η  = F . d / A .ⅴ

Where:

•   F is the force required to maintain a unit velocity gradient between two parallel layers of liquid of a unit area.
•   d is the distance between the two layers of liquid skidding over each other
•   A is the area
•    ⅴ is the velocity.

The coefficient of viscosity is a measure of how easily or difficult a fluid flows under the effect of external forces, and it plays a very important role in many industrial, scientific, and everyday applications.

Examples of Coefficient of Viscosity 

1. Water: The coefficient of viscosity for water at 20°C is nearly 0.001 Pa·s (pascal-seconds) or 1 centipoise (cP). This is considered a relatively low viscosity that allows water to flow easily and is one of the reasons why it is commonly used for viscosity comparisons.
2. Honey: The coefficient of viscosity for honey can range from 10 to 20 Pa·s or higher, depending on factors such as the honey type and the temperature. This high viscosity gives honey its thick and slow-flowing characteristic.
3. Motor Oil: The coefficient of viscosity for motor oil has a wide range, from 20 to 100 centistokes (cSt) or higher. Motor oil is designed to have a higher viscosity compared to water and this ensures effective lubrication of engine components. Higher-viscosity oils have higher coefficients of viscosity.
4. Air: Gases also have a coefficient of viscosity. The coefficient of viscosity for air at atmospheric pressure or room temperature is approximately 0.000018 Pa·s or 0.018 millipoise (mP). The viscosity of gases is considerably lower than that of fluids and this low viscosity allows air to flow easily.

5.   Molten Glass: The coefficient of viscosity for molten glass can range from around 10^2 to 10^8 Pa·s, indicating a high resistance to flow. And this depends on its temperature and composition.

The Coefficient of Viscosity Using Stoke’s Method

Stoke’s method or Stoke’s law is a mathematical equation that expresses the velocities of the small spherical objects in a fluid medium and says that any object when rises or falls through a fluid it will experience a frictional or drag force because of the fluid. 

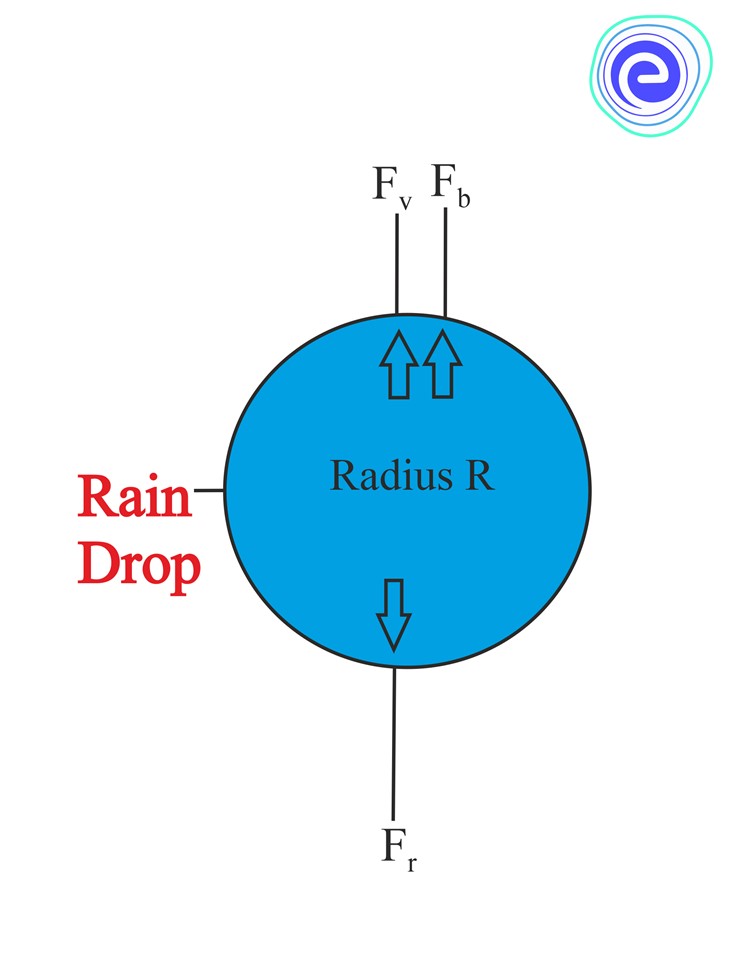
 In other words,  Stoke’s law states that the force of viscosity on a small sphere moving through a viscous fluid is given by the following equation:

F=6πμrv

Where:
F is the frictional force acting on the interface between the fluid and the particle.
μ is the dynamic viscosity
r is the radius of the spherical object
V is the flow velocity relative to the object

Importance of Stoke’s Law

• Stoke’s law is important in explaining the formation of clouds, the falling from a parachute, why the larger rain droplets hurt more than the smaller ones, and more.

Millikan depended on the concept of Stokes’ law in his oil-drop experiment, which was used to determine the electronic charge.

PraxiLabs, the 3D virtual lab solution, provides students with access to realistic biology, chemistry, and physics labs and enriches their understanding with a variety of informational and educational content .. Pick the best plan for you now!

 

Stoke’s Law Derivation

The viscous force acting on a sphere is directly proportional to the following factors:

Coefficient of viscosity (η) as F ∝ ηa  …(i)

The radius of the sphere (r) as F ∝  rb …(ii)

The velocity of the object (v) as F ∝ vc …(iii)

Combining the above three equations we get,

F ∝ ηa rb vc

Removing the proportionality sign and adding the proportionality constant k we get.

F = k ηa rb vc……(1)

Now, equating the dimensions of parameters on either side of equation (1)

[MLT–2] = [ML–1T–1]a [L]b [LT-1]c

Simplifying the above equation,

[MLT–2] = [Ma ⋅ L–a+b+c ⋅ T–a–c]……(2)

Equating the superscripts of mass, length, and time respectively from equation (2), we get

a = 1 ….(a)

–a + b + c = 1 ……(b)

–a –c = 2

a + c = 2 ……(c)

from (b), (c)

1 + c = 2

c = 1  ……(d)

from (a) & (b) in (d), we get

–1 + b + 1 = 1

b = 1 ……(e)

From (a), (d), and (e)

F = k η r v

For any spherical body, the value of k was experimentally obtained to be 6π. 

Thus, the viscous force on a spherical body falling through a liquid is given by the equation, F = 6πηrv

Source

Determination of the Coefficient of Viscosity by Stoke’s Method Experiment From PraxiLabs

PraxiLabs provides a virtual lab simulation for the experiment (Determination of the Coefficient of Viscosity by Stoke’s Method)

Learning Objectives

By the end of the determination of the coefficient of viscosity using Stoke’s method experiment, the students should be able to:

1. Understand the definition of the viscosity.
2. Detect the CGS and MKS (SI) units for measuring the coefficient of viscosity.
3. Explain the origin of the viscosity in both liquids and gases.
4. Estimate the temperature effect on the coefficient of viscosity for fluids and enumerate the other different factors that could change the viscosity of a liquid.
5. Set up an experiment to measure the coefficient of viscosity of liquids.

In this experiment, we will need:

Cylindrical glass jar – Steel balls of different radii – Highly viscous liquids – Ruler – Stopwatch.

The experiment of determination of the coefficient of viscosity depends on measuring the fall-terminal speed of a metal sphere that falls in a glass jar filled with a viscous fluid, as a function of the sphere’s radius. Hence the viscosity coefficient of the liquid can be readily determined.

PraxiLabs provides properties of matter virtual labs to students and educators that include a set of hands-on experiments designed to support students’ understanding of the principles of physics. Subscribe now!

 

Theoretical Background

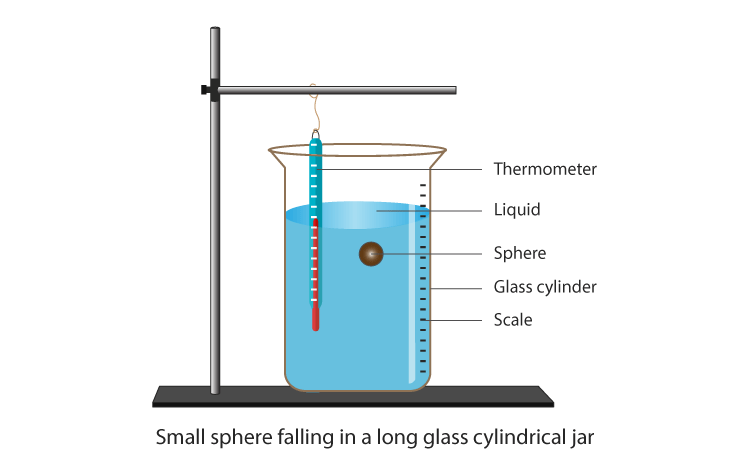
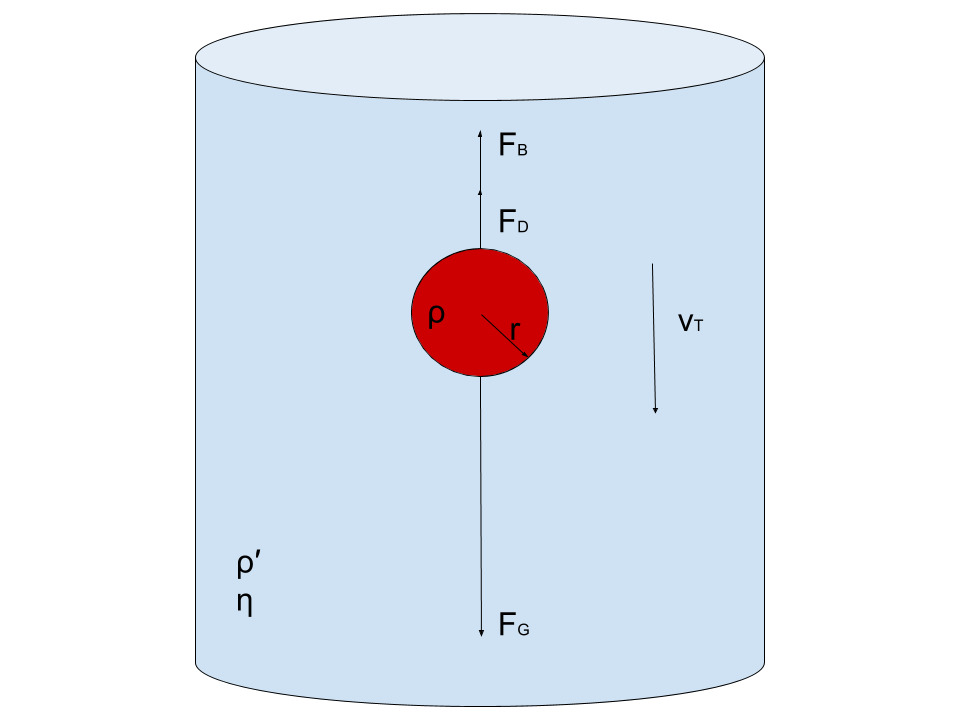
Consider a steel ball of radius (r) is released from the top of a glass jar filled with a viscous fluid with viscosity coefficient (η). The instant the ball hits the liquid’s surface, it stops momentarily and then begins to accelerate downward under the effect of gravity.

At the same time, the so-called viscous force ( Fv) begins to oppose the motion of the ball, as it depends directly on the speed of the ball (see eq.(3)). As time goes on, the viscous force (which is also called the drag force or Stoke’s force) increases in magnitude until it reaches a value together with the buoyant force that balances the weight of the ball.

Theory In such a case, the ball moves with a constant speed called the terminal velocity ( vo or sedimentation velocity). Before reaching the bottom of the jar, the ball decelerates and eventually comes to a stop. This means that within a certain length of the jar away from its ends (both are marked on the glass jar with two marks A and B), the ball moves with a uniform speed, under the effect of three balanced forces:

1- The Ball Weight

Where:

 mball is the mass of the ball

 g is the acceleration due to gravity

 Vball is the volume of the ball.

And ρball is the density of the ball’s material.

2- Upthrust force (or the buoyant force)

Upthrust force is the force exerted by the fluid on the immersed body and acting upward. Recall that the buoyant force equals the weight of the immersed body:

Where ρliquid is the density of the liquid’s material. However, since the volume of immersed body Vball equals the volume of displaced liquid Vliquid,

3- Viscous force

Viscous force acting the ball due to the viscosity of the liquid ?, acts upward,

However, when the ball moves with the terminal velocity vo , the net force acting on the ball is zero; then

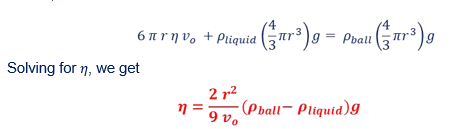
Effect of the Jar’s Wall

To take into account the proximity of the jar’s wall which affects the motion of the ball, the terminal speed vo can be calculated to the first approximation using the relation

Where R is the inner radius of the jar and v is the measured velocity.

Effect of Temperature

The viscosity coefficient depends on the fluid’s temperature. As the temperature increases, the coefficient of the viscosity decreases for liquids and increases for gases.

This can be interpreted according to the origin of viscosity in both. For liquids, the viscosity originates from the frictional force between adjacent layers when they move past each other, therefore increasing temperature, and causes the separation distance between layers to increase and the viscosity decrease.

 On the other hand, in gases, the viscosity originates from the collisions made by the gas molecules with each other within the same layer. Increasing the temperature causes these collisions to increase and the viscosity increases as well.

The steps of the Experiment

In PraxiLabs virtual lab of the determination of Coefficient of Viscosity Using Stoke’s Method experiments, you will do the following steps to conduct the experiment successfully

1. Choose a liquid from the drop list, such as glycerin.
2. Select the ball’ radius from the slide bar.
3. Adjust the distance between the two movable marks “A” and “B” (10 – 90 cm).
4. Click on the “Drop Ball” button to drop the solid ball inside the jar. When the ball reaches the mark “A”, Click the “Start” button to start the stopwatch.
5. When the ball (inside the red circle) reaches the mark “B”, click the “Stop” button. 6. Click the “Record” button to record this time.
6. Click the “New Trial” button to start over with the same ball if you want.
7. Repeat the previous steps for all the available ball’ radii.
8. The experiment has ended, an Excel sheet will be downloaded that contains the data you’ve recorded.
9. You will calculate r (m) and r 2 (m2) / the apparent speed of the ball / the terminal speed of the ball.
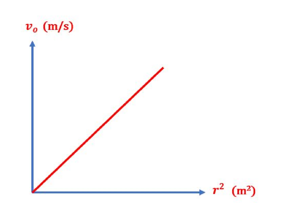
10. Plot a relation between vo and r 2 , which should yield a straight line that passes through the origin, then calculate the slope of the line.

11. Finally, Calculate the viscosity coefficient of the chosen liquid using the following relation:

Now, you can easily conduct (determination of the Coefficient of Viscosity by Stoke’s Method Experiment) on your own for free. Create your free account and try it now!